Is mt_rand() really random?

To obtain a pseudo-random number using PHP's random-number generator, call the mt_rand() function and it will return a value between 0 and RAND_MAX in which RAND_MAX is a system-defined upper limit (which you can inspect by calling the mt_getrandmax() function).

The mt_rand() function uses the Mersenne Twister algorithm and is four times faster and better characterized than PHP's older rand() function.

Before you use PHP's mt_rand() in your probability models, you might want to convince yourself that the mt_rand() function works correctly. How could you do this?

Most developers are content to write a script, get it to generate a few random values, and then accept that it is working correctly if they don't notice any obvious biases in the numbers that are appearing. This eyeball analysis might convince you, but it won't, as they say, convince the lawyers.

One approach to find more convincing evidence is to precisely define what it means for a sequence of numbers to be random. A random sequence of numbers should have many properties, but one of the most important properties is that each number in the range of possible values should have an equal likelihood of appearing at each point in the sequence.

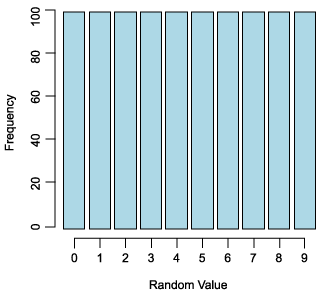
A way to measure whether this is true is by counting the number of times each value occurs and graphing the frequency counts for each value. The resulting graph should approximate a uniform distribution of counts for each value in your range. If you limit the range of allowable sequence numbers from 0 to 9 and generate a sequence of 1,000 numbers, then the graph should approximate the discrete uniform distribution depicted in Figure 5.

Figure 5. Uniform distribution for truly random numbers

To test whether PHP's mt_rand() function generates a uniform distribution of random values, I've created a script that uses the Chi Square test to determine this. The first half of the script is primarily concerned with creating a frequency distribution from output of mt_rand(). The second half performs the ChiSquare test.

The test involves setting the alpha cutoff to use for computing a critical Chi Square value. If the obtained Chi Square value exceeds the critical Chi Square value, then you would reject the null hypothesis that the mt_rand() values come from a uniform distribution. In fact, you would not reject the null hypothesis if mt_rand() is working as it should.

<?php 

/**
* @package PHPMath_ChiSquare
*/

require_once "PHPMath/ChiSquare/ChiSquare1D_HTML.php"; 

/**
* Script tests whether mt_rand function generates a sequence of
* values that can be fit to a discrete uniform distribution 
* @version 1.0
* @author Paul Meagher
*/

// Set range of random values that you want to generate
$Low  = 0;     
$High = 9;     

// Set number of random values you want to generate 
$Iterations = 1000;   

// Zero the frequency distribution array
$FreqDist = array(); 

// Compute probability of each range value
$NumVals = count(range($Low, $High)); 
$Prob    = 1 / $NumVals; 

for($i = 0; $i < $Iterations; $i++) { 
  $RandValue = mt_rand($Low, $High); 
  $FreqDist[$RandValue]++; 
} 

for($i=0; $i < $NumVals; $i++) { 
  $ObsFreq[$i] = $FreqDist[$i + $Low]; 
  $ExpProb[$i] = $Prob;   
}   

$Alpha    = 0.05; 
$Chi      = new ChiSquare1D_HTML($ObsFreq, $Alpha, $ExpProb); 
$Headings = range($Low, $High); 
echo "<p>". $Chi->showTableSummary($Headings) ."</p>";
echo "<p>". $Chi->showChiSquareStats() ."</p>";

?> 

The following table shows a sample output from this script. As the obtained Chi Square value of 7.90 is less than the critical value of 16.92, you cannot reject the null hypothesis that your observed frequencies are different than the frequencies expected under the assumption that you are sampling from a uniform distribution.

Table 1. Output from PHP Chi Square script

It can be instructive to run this script a number of times and observe that on some occasions you reject the null hypothesis. Why do you think this occurs? How often can this occur before you need to reject the null hypothesis? And is there a tool to help make these determinations?